파동(wave) [1]

Samsung Semiconstroy Global (삼성전자도 잘못 표기한다.)

[휴대폰으로 보면 LaTeX이 그대로 표시됩니다. PC를 사용하시길 권장 드립니다.]

 

시작은 왜 한 파장에 대하여 주기(period)와 파장(wavelength)이라는 개념을 섞어 사용하는지에 대한 의문에서부터였다.

분명 주기의 단위는 시간(s)이며 파장의 단위는 길이(m)인데 이들이 한 그래프에 함께 표기되어 있는 것이다.

그리고 분명 \(x\)축이 시간인데 왜 파장의 단위는 길이가 되는지 의문은 갈수록 커져만 갔다.

결국 수능특강 물리II를 꺼내들어 밑바닥부터 정리해보았다.

 

지금부터 우리는 공에 끈을 묶은 채 일정한 속도로 회전 운동을 하는 사고 실험을 할 것이다.

따라서 공은 일정한 속도로 원운동을 할 것이다. 그리고 삼각함수, 보통은 sine 그래프를 그릴 것이다.

그런데 여기서 우리는 총 2개의 domain으로 나눠 생각해볼 수 있다.

바로 시간 영역(Time domain)과 공간 영역(Space domain)이다.

그리고 이제부터 각각의 영역(domain)에 대해 차근차근 알아보도록 하자.

 

[1] Time domain-(1)

가장 직관적이다.

처음에는 축 쳐져있을 공이 회전 운동을 하면 최고점으로 올라가고 다시 끈의 장력 때문에 내려오길 반복할 것이다.

그럼 쉽게 삼각함수(sine 또는 cosine) 그래프가 그려질 것이다.

그리고 주기라는 개념을 도입하면 공이 자신이 원래 있던 위치로 돌아오는데 걸리는 시간 정도가 되겠다.

네이버 물리학백과에 따르면 주기(period)의 정의는 아래와 같다.

"진동이나 파동이 일정한 간격을 두고 반복되는 현상에서 반복이 일어나는데 걸리는 시간 간격을 주기라 한다."

 

그리고 각속도(angular velocity) \(\omega~\) 를 도입한다.

\(2\pi\)라는 각도는 360도이며 이는 원을 정확히 한 바퀴 돌렸음을 의미한다.

이때 주의해야 하는 점은 각속도(\(\omega\))와 속도(\(v\))는 다르다는 점이다.

속도(\(v\))는 원의 반지름이 바뀌면 달라진다.

$$\ell=r\theta$$

$$\frac{d\ell}{dt}=\theta\frac{dr}{dt}+r\frac{d\theta}{dt}$$

 

원의 반지름이 일정하다고 가정하면 (또는 단위원, unit circle이라 가정하자.)

$$\vec{v}=\frac{d\ell}{dt}=r\frac{d\theta}{dt}=r\omega$$

 

따라서 \(2\pi\)를 도는데 시간이 얼마나 걸렸는지를 하나의 식으로 정리하면 아래와 같다. 

$$T=\frac{2\pi}{\omega}$$

 

식을 보면 자연스럽게 각속도가 증가하면 분모가 증가하여 주기(T)가 짧아짐을 알 수 있다.

 

[1-2] Time domain-(2)

다르게 생각해볼 수도 있다.

그래프 상으로 보면 주기는 시간 단위이고 그래프의 \(x\)축에 해당한다.

따라서 단위를 생각하면 \(x\) 역시 시간을 단위로 가져야 한다.

동시에 주기란 \(2\pi\)의 배수이므로 아래와 같이 식을 쓸 수 있다.

\(t\)라는 시간 동안 \(n\)바퀴를 돈 것이라 생각할 수 있다. (당연하지만 바퀴는 당연히 정수배이다.)

$$T=\frac{2\pi t}{n}$$

 

그리고 위 식에서 식 일부를 아래와 같이 정리해보자.

$$\frac{t}{n}=\frac{1}{\alpha}~\Rightarrow~\alpha=\frac{n}{t}$$

식을 말로 풀어보자면 \(t\)시간 당 \(n\)바퀴 돌았음을 의미한다.

 

이때 \(n=1~\)일 경우 \(t\)는 자연스럽게 \(T\)가 되어 식은 아래와 같이 정리된다.

$$\alpha=\frac{1}{T}=f$$

바로 진동수(\(f\), frequency)가 된다.

 

또는 한 바퀴를 수학적으로 표현하여 \(2\pi\)라 하면 각속도가 그대로 나옴을 볼 수 있다.

$$\omega=\frac{2\pi}{T}$$

 

[2] Space domain

space domain은 원운동으로 해석하기 조금 힘들다. (물론 마지막에는 원으로 설명이 마무리될 것이다.)

따라서 로프웨이브(ropewave) 또는 배틀로프(battle rope) 운동을 생각해야 한다.

그리고 로프웨이브 운동을 하고 있는 사람을 사진기로 찍으면 시간은 고정되는 효과를 볼 수 있다.

반대로 앞서 살펴본 원운동은 옆에서 보면 원운동이지만 회전면과 수직이 아닌 평행한 방향으로 보면 위치가 고정된다.

그럼 자연스럽게 사진 위에 자를 두고 길이를 측정하면 된다.

그 길이가 바로 파장(wavelength)이다.

하지만 이걸로는 수식으로 표현하기 부족하다. (그래서 이틀을 더 고민했다.)

 

Coach Mag

그러니 여기서 한 걸음 더 나아가보도록 하자.

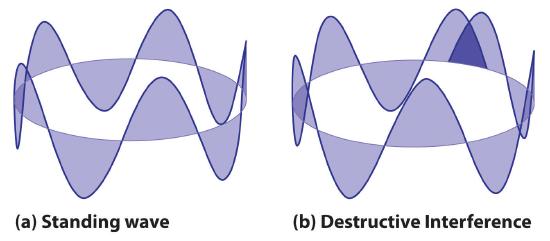
뜬금없지만 드 브로이(De Broglie)의 물질파(matter wave)를 가져온다.

우리의 경우에는 로프웨이브의 양단을 연결해주면 된다.

이렇게 하면 로프웨이브의 길이는 원의 둘레길이인 \(2\pi r\)로 표현이 가능해진다.

그리고 그 안에서 몇 개(n)의 파장이 있는지는 아래와 같은 식으로 표현이 가능하다.

$$\lambda=\frac{2\pi r}{n}$$

 

Chemistry LibreTexts

Science Ready

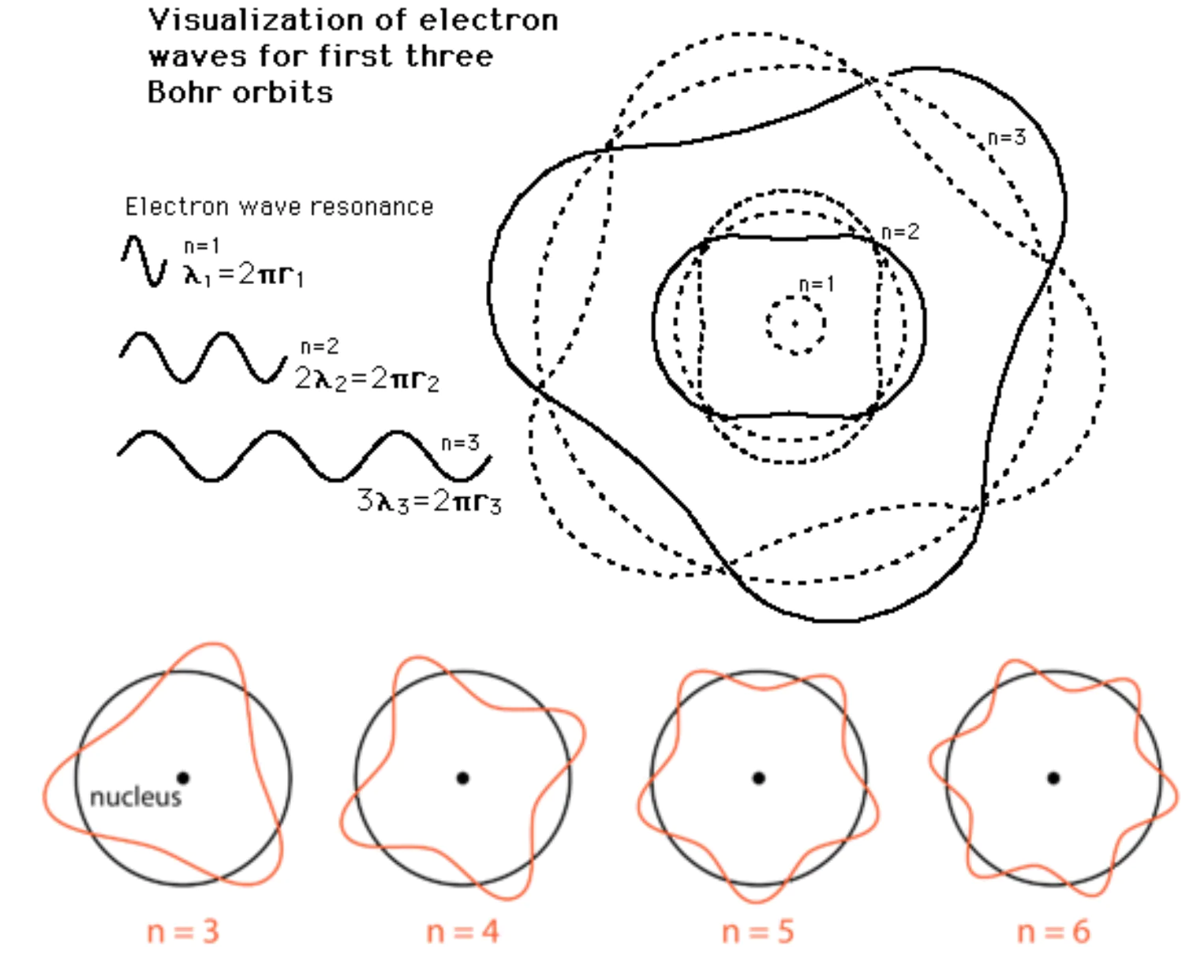
당연히 주기와 마찬가지로 파장도 원의 반지름이 변하면 달라진다.

따라서 지름은 단위 원(unit circle)이라 가정한 채 고정하고 갯수(n)만 바꾸도록 한다.

그럼 식은 아래와 같다.

$$\lambda=\frac{2\pi}{n}$$

 

그리고 우리는 계속 몇 개가 있는지를 n이라 표현했음을 기억하자.

'n'이라 말했듯이 개수는 영어로 number가 되고 이는 파장의 number이므로 wavenumber가 된다.

그리고 물리학에서 wavenumber는 \(\kappa\)로 표현한다.

따라서 식은 최종적으로 아래와 같이 쓸 수 있다.

$$\lambda=\frac{2\pi}{\kappa}$$

 

식을 보면 자연스럽게 단위원을 잘개 쪼갤수록 파장(wavelength)이 짧아짐을 알 수 있다.

 

그리고 무려 최종적으로 우리는 이 두 영역을 하나의 영역(domain)으로 합칠 수 있다.

바로 phasor domain이다. 직관적으로 느껴볼 수 있는 방법은 geogebra에 아래와 같이 입력해보면 된다.

 

$$z=A\sin(x)~~~~~z=A\sin(y)$$

 

이때 \(x~\)는 time-domain \(y~\)는 space domain이라 할 경우 물결치는 파도가 나온다.

그리고 해당 파도는 \(y=x\)를 따라 진행됨을 볼 수 있어 \(y=x\)를 축으로 하는 새로운 삼각함수가 등장한다.

이에 대해서는 다음 글에서 자세히 다뤄보도록 하자.