대학원 공부노트
파동(wave) [2] 본문

지난 내용에서 파동은 시간 영역과 공간 영역으로 나눠짐을 확인하였다.
그리고 말미에 이 둘을 하나로 통합할 수 있는 phase domain에 대해 짧게 소개했다.
오늘은 이 phase domain에 대해 자세히 알아보고자 한다.
(phase domain은 제가 임의로 정한 이름이니 주의 바랍니다.)
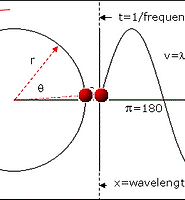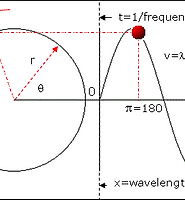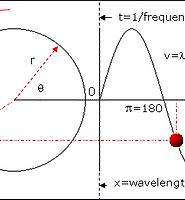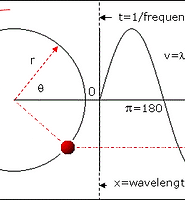
우선 time domain과 space domain의 원점을 합친다.
앞선 글에서 반지름의 길이가 1인 단위원을 도입하였으므로 원점을 통일하여도 크게 문제될 게 없다.
그러면 아래와 같이 \(z\)축은 amplitude를, \(x\)축은 시간을, \(y\)축은 공간을 나타낸다.
(이때 '공간' 상으로 퍼져 나가는 음파와 내가 말하는 '공간'축은 동일한 개념이 아니니 주의하자.)
$$t=\frac{T}{\lambda}x$$
$$T=\frac{2\pi}{\omega}~~~\lambda=\frac{2\pi}{k}$$
$$t=\frac{2\pi}{\omega}\frac{k}{2\pi}x=\frac{k}{\omega}x$$
식을 적절하게 정리해주면 아래와 같아진다.
$$\omega t = k x$$
$$\omega t -k x =0$$
원점에서만 시작하지 않는다면 식은 아래와 같이도 표현할 수 있다.
$$\omega t-k x=\phi=\rm{const}$$
이렇게 하면 재미있는 식 두 개를 얻을 수 있다.
$$\frac{\partial \phi}{\partial t}=\omega$$
$$\frac{\partial \phi}{\partial x}=-k$$
그리고 고등학교 때 직선의 방정식과 평면의 방정식을 기억한다면 해당 식에 물리적 의미를 부여할 수 있게 된다.
평면의 방정식은 아래와 같다.
$$a(x-x_{0})+b(y-y_{0})+c(z-z_{0})+d=0$$
우리의 경우에는 \(z\)방향이 없으므로 세 번째 항을 생략할 수 있다.
$$a(x-x_{0})+b(y-y_{0})+d=0$$
그리고 해당 평면은 원점\((x_{0}=0,y_{0}=0)\)을 포함하므로 \(d=0\)이다.
$$ax+by=0$$
그리고 우리는 \(x-y\) 좌표계가 아닌 \(x-t\) 좌표계이며 계수는 \(a\)와 \(b\)가 아닌 \(k\)와 \(\omega\)이다.
그렇게 하면 우리가 위에서 다루었던 식이 그대로 나온다.
즉, 우리가 구한 방정식은 아래 사진과 같은 constant phase surface(=plane) 방정식이다.

이쯤에서 그럼 우리가 왜 이렇게 고생하면서 파동(wave)을 다루었는지 알 수 있다.
파원(wave source)에서 나오는 파동(wave)를 시간과 공간을 포함한 3차원의 식으로 표현하기 위함이다.
(나중에 기회가 된다면 적절한 삽화를 직접 그려 넣고 싶다.)
왜냐하면 time-domain과 space-domain을 합친 그래프가 아래와 같기 때문이다.
$$p=A\sin(\omega t-k x)$$
당연히 sine 함수는 cosine 함수로 대체할 수 있다.
$$p=A\cos(\omega t- kx)\cdots(1)$$
그리고 식 (1)은 다시 아래와 같이 표현해도 무방하다.
$$e^{i\phi}=cos\phi+i \sin\phi$$
$$\phi=\omega t-kx$$
$$\mathbb{R}[e^{i\phi}]=\cos\phi~~~\Rightarrow~~~A\cos(\omega t-kx)$$
$$p=A e^{i\phi}=A e^{i(\omega t-kx)}$$
This equation means a plane wave traveling with amplitude \(A\) in the positive \(x\) direction.
Reference
Acoustics and Vibration Animations, Plane-Wave Partial-Wave Expansion
TEM theory without too much mathematics, The scattering vector and plane waves in 3D
Wave-Particle Duality, Wavefunctions by farside.ph.utexas.edu
Wave-Particle Duality, Representation of Waves via Complex Functions by farside.ph.utexas.edu
Hyperphysics, String Wave Solutions and etc.
조금은 느리게 살자, 균일 평면파의 의미(Uniform Plane Wave) [2012]
네이버 블로그, 듀올스 「[Chpater 2. Wave Motion] (1) One-Dimensional Waves (2016)
네이버 블로그, 듀올스 「[Chapter 2. Wave Motion] (4) Plane Waves and Three Dimensional Waves (2016)
네이버 블로그, 미이라 「(추가)Fundamentals of Plane Wave」(2016)
'공학 > 대학물리' 카테고리의 다른 글
| 원운동 1편 (0) | 2022.12.27 |
|---|---|
| Speed of sound (0) | 2022.09.18 |
| Momentum (0) | 2022.09.17 |
| 파동(wave) [1] (0) | 2022.07.29 |