Hasegawa(1969) 8번, 10번, 11식 해설

04-14 12:28

« 2025/04 »
일	월	화	수	목	금	토
		1	2	3	4	5
6	7	8	9	10	11	12
13	14	15	16	17	18	19
20	21	22	23	24	25	26
27	28	29	30

Archives

Today

Total

관리 메뉴

대학원 공부노트

Hasegawa(1969) 8번, 10번, 11식 해설 본문

대학원 공부/Hasegawa

Hasegawa(1969) 8번, 10번, 11식 해설

lightbulb_4999 2022. 7. 20. 17:00

[해당 페이지는 휴대폰이 아닌 컴퓨터로 보시길 적극 권장 드립니다.]

오늘 다룰 내용은 전적으로 새로운 수학적 기술을 사용해야 할 필요가 없는 평이한 내용을 다룰 것이다.

다만 값이 조금 복잡해 부호 하나만 틀려도 꽤나 애먹는 그런 내용이다.

그리고 아쉽게도 식(8)이 어떻게 나온 것인지에 대한 설명은 담고 있지 않다.

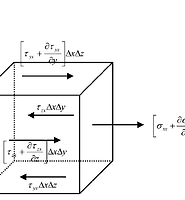
$c_{n} = - \frac{[F_{n} j_{n} (x) - x j_{n}^{'} (x)]}{[F_{n} h_{n}^{(2)} (x) - x h_{n}^{(2)'} (x)]} \dots (a)$

우리가 기본적으로 사용할 flow는 아래와 같다.

$c_{n} = \frac{c}{a + b i}$

$= \frac{c (a - b i)}{(a + b i) (a - b i)}$

$= \frac{c (a - b i)}{a^{2} - b^{2} i^{2}}$

$= \frac{c (a - b i)}{a^{2} + b^{2}}$

$= \frac{a c}{a^{2} + b^{2}} - i \frac{b c}{a^{2} + b^{2}} \dots (b)$

그리고 논문에서 주어진 식은 다음과 같다.

$c_{n} = α_{n} + i β_{n}$

$α_{n} = - \frac{{[F_{n} j_{n} (x) - x j_{n}^{'} (x)]}^{2}}{{[F_{n} j_{n} (x) - x j_{n}^{'} (x)]}^{2} + {[F_{n} n_{n} (x) - x n_{n}^{'} (x)]}^{2}}$

$β_{n} = - \frac{[F_{n} j_{n} (x) - x j_{n}^{'} (x)] [F_{n} n_{n} (x) - x n_{n}^{'} (x)]}{{[F_{n} j_{n} (x) - x j_{n}^{'} (x)]}^{2} + {[F_{n} n_{n} (x) - x n_{n}^{'} (x)]}^{2}}$

더럽게 복잡하지만 일정한 위 $(b)$ 식과 함께 보면 일정한 규칙이 있음을 알 수 있다.

$a = [F_{n} j_{n} (x) - x j_{n}^{'} (x)]$

$c = - [F_{n} j_{n} (x) - x j_{n}^{'} (x)]$

$b = [F_{n} n_{n} (x) - x n_{n}^{'} (x)]$

$α = \frac{a c}{a^{2} + b^{2}}$

$β = \frac{b c}{a^{2} + b^{2}}$

$c_{n} = \frac{a c}{a^{2} + b^{2}} + i \frac{b c}{a^{2} + b^{2}} (a = - c)$

그리고는 영화 테넷처럼 역으로 거슬러 올라가보자.

$c_{n} = \frac{a c}{a^{2} + b^{2}} + i \frac{b c}{a^{2} + b^{2}}$

$= \frac{a c + i (b c)}{a^{2} + b^{2}}$

$= \frac{c (a + b i)}{a^{2} + b^{2}}$

$= \frac{c (a + b i)}{(a + b i) (a - b i)}$

$= \frac{c}{a - b i}$

그대로 $a, b, c$ 값을 대입해주면

$c_{n} = - \frac{F_{n} j_{n} (x) - x j_{n}^{'} (x)}{[F_{n} j_{n} (x) - x j_{n}^{'} (x)] - i [F_{n} n_{n} (x) - x n_{n}^{'} (x)]}$

이때 식 $(a)$ 에서 등장하는 $h_{n}^{(2)} (x)$ 는 Hankel function이며 다음과 같이 풀어 쓸 수 있다.

(Hankel function에 대한 자세한 이야기, 왜 이렇게 되는지는 다음에 다루도록 한다.)

$h_{n}^{(2)} (x) = j_{n} (x) - i n_{n} (x)$

Hankel function에 맞춰 우리가 처음 시작한 $a$ 와 비슷하게 만들어주면 아래와 같아진다.

$c_{n} = \frac{F_{n} j_{n} (x) - x j_{n}^{'} (x)}{F_{n} [j_{n} (x) - i n_{n} (x)] - x [j_{n}^{'} (x) - i n_{n}^{'} (x)]}$

$c_{n} = - \frac{[F_{n} j_{n} (x) - x j_{n}^{'} (x)]}{[F_{n} h_{n}^{(2)} (x)] - x [j_{n}^{'} (x) - i n_{n}^{'} (x)]}$

그리고 여기서 Bessel function, Neumann function, Henkel function의 미분형을 도입한다.

(왜 아래와 같은 식이 나왔는지는 다음에 다루도록 한다.)

$j_{n}^{'} (x) = - \frac{(n + 1)}{x} j_{n} (x) + j_{n - 1}^{'} (x)$

$n_{n}^{'} (x) = - \frac{(n + 1)}{x} n_{n} (x) + n_{n - 1}^{'} (x)$

$h_{n}^{(2)'} (x) = - \frac{(n + 1)}{x} h_{n}^{(2)} (x) + h_{n - 1}^{(2)'} (x)$

그대로 대입해주면 아래와 같아진다.

하지만, 식이 길어지므로 다음부터는 일부만 담아 전개하였다.

$c_{n} = - \frac{[F_{n} j_{n} (x) - x j_{n}^{'} (x)]}{[F_{n} h_{n}^{(2)} (x)] - x [(- \frac{(n + 1)}{x} j_{n} (x) + j_{n - 1} (x)) - i (- \frac{(n + 1)}{x} n_{n} (x) + n_{n - 1} (x))]}$

$- \frac{(n + 1)}{x} [j_{n} (x) - i n_{n} (x)] + [j_{n - 1} (x) - i n_{n - 1} (x)]$

$= - \frac{(n + 1)}{x} h_{n}^{(2)} (x) + h_{n - 1}^{(2)} (x)$

$= h_{n}^{(2)'} (x)$

$c_{n} = - \frac{[F_{n} j_{n} (x) - x j_{n}^{'} (x)]}{[F_{n} h_{n}^{(2)} (x) - x h_{n}^{(2)'} (x)]}$

결국, 최종적으로 얻게 되는 식은 제일 처음 소개된 식과 동일함을 볼 수 있다.

참고자료

Wikipedia, Bessel function

Mathematics Stack Exchange, 'Anyone know who to take the 2nd derivative of a spherical bessel function?'

'대학원 공부 > Hasegawa' 카테고리의 다른 글

Hasegawa equation (0)	2022.08.05
Hasegawa(1969) 1번 식 해설 4편(완) (0)	2022.07.31
Hasegawa(1969) 1번 식 해설 3편 (0)	2022.07.29
Hasegawa(1969) 1번 식 해설 2편 (0)	2022.07.26
Hasegawa(1969) 1번 식 해설 1편 (0)	2022.07.25