Hasegawa(1969) 1번 식 해설 1편

Pixabay

[해당 페이지는 휴대폰이 아닌 컴퓨터로 보시길 적극 권장 드립니다.]

 

Hasegawa 논문에서 입자는 rigid가 아닌 elastic이라 상정하였으므로 음파에 노출되었을 때 변형이 일어난다.

따라서 입자의 변형(deformation)을 해석하고자 고체역학에서 배운 개념을 도입할 것이며 시작은 용어 정리이다.

 

전단응력 shear stress: $\tau$

수직응력 normal stress: $\sigma$

전단변형률 shear strain: $\gamma$

수직변형률 normal strain: $\epsilon$

텐서표기법 tensor notation: ${\tau }_{xy}$

> $x$를 법선벡터(normal vector)로 가지는 평면에 $y$ 방향으로 가하는 힘이다.

 

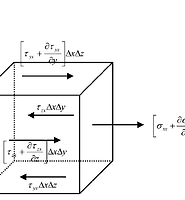
그리고 이를 바탕으로 미소체적(infinitesimal volume)에 힘이 어떻게 인가되는지 알아보도록 하자.

정육면체는 총 6개의 면을 가지며 서로 마주하는 변을 하나로 보면 총 3개의 면(surface)을 가진다.

그리고 하나의 면에는 면에 수직인 힘과 면과 평행한 방향으로 작용하는 두 종류의 힘, 이렇게 총 3 종류의 힘이 존재한다.

따라서, 정육면체에는 총 9가지 방향의 힘을 고려할 수 있다.

 

 

이를 행렬(matrix)로 나타내면 아래와 같다.

 

$$\epsilon =\left[\begin{array}{ccc}{\epsilon }_{xx}& {\epsilon }_{xy}& {\epsilon }_{xz}\\ {\epsilon }_{yx}& {\epsilon }_{yy}& {\epsilon }_{yz}\\ {\epsilon }_{zx}& {\epsilon }_{zy}& {\epsilon }_{zz}\end{array}\right]=\left[\begin{array}{ccc}{\epsilon }_{xx}& \frac{1}{2}{\gamma }_{xy}& {\gamma }_{xz}\\ \frac{1}{2}{\gamma }_{yx}& {\epsilon }_{yy}& \frac{1}{2}{\gamma }_{yz}\\ \frac{1}{2}{\gamma }_{zx}& \frac{1}{2}{\gamma }_{zy}& {\epsilon }_{zz}\end{array}\right]$$

 

그리고 지금부터는 위 행렬이 어떻게 나왔는지에 대해 알아볼 것이다.

전단응력을 고려하기 위해 원점 $O$에서의 속도와 $x$축 위의 임의의 한 점 $A$에서의 속도가 다르다고 가정하자.

그리고 $x$ 방향의 속도는 $u$, $y$ 방향의 속도는 $v$ 라 가정하자.

그럼 원점 $O$는 좌표계에서 $(x_0,y_0)$이므로 이곳에서의 $y$ 방향의 속도는 다음과 같이 표기할 수 있다.

$$v_0=v(x_0,y_0)\approx v(x_0)$$

 

마찬가지로 임의의 한 점 $A$는 $A(x_0+dx,y_0)$이므로 이곳에서의 속도는 아래와 같다.

$$v_A=v(x_0+dx,y_0)\approx v(x_0+dx)$$

 

여기에 테일러 전개(Taylor expansion)을 적용해주면 다음과 같이 풀어 쓸 수 있다.

$$v(x_0+dx,y_0)=v(x_0,y_0)+\frac{\partial v_0}{\partial x}dx$$

 

따라서 원점과 임의의 한 점 간의 속도 차이는 아래와 같다.

$$v_A-v_0=\frac{\partial v_0}{\partial x}dx$$

 

그리고 '거리'는 '속력에 시간을 곱한 것'이므로 상단부만 밀린 경우 밀린 '거리'는 아래와 같다.

$$s=\frac{\partial v_0}{\partial x}dx\times dt$$

 

그리고 밀린 '정도'를 보기 위해 각도를 도입하도록 한다.

이때 $\alpha \approx \tan \alpha$라 할 수 있으므로 아래와 같이 정리할 수 있다.

$$\alpha \approx \tan \alpha =\frac{\frac{\partial v_0}{\partial x}dx\times dt}{dx}=\frac{\partial v_0}{\partial x}dt$$

 

여기서 단위를 보면 길이 단위를 길이로 나누어주었으므로 단위가 없는 무차원수임을 알 수 있다.

그리고 시간 당 변형률(shear strain rate)는 다음과 같다.

$$\frac{d\alpha }{dt}=\frac{\partial v_0}{\partial x}$$

---

동일한 계산을 원점 $O$와 $y$축 위의 임의의 한 점 $B$ 사이에서 수행한다.

$$u_0=u(x_0,y_0)$$

$$u_B=u(x_0,y_0+dy)=u(x_0,y_0)+\frac{\partial u_0}{\partial y}dy$$

$$u_B-u_0=\frac{\partial u_0}{\partial y}dy$$

$$\beta \approx \tan \beta =\frac{\frac{\partial u_0}{\partial y}dy\times dt}{dy}=\frac{\partial u_0}{\partial y}dt$$

$$\frac{d\beta }{dt}=\frac{\partial u_0}{\partial y}$$

 

그리고 이 둘에 대한 평균 shear strain rate를 구해주면 $xy$ 평면에 대한 변형률을 구할 수 있다.

$${\epsilon }_{xy}=\frac{1}{2}(\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y})=\frac{1}{2}{\gamma }_{xy}$$

 

동일한 방법을 다른 평면에도 적용해주면 다음과 같다.

$${\epsilon }_{yz}=\frac{1}{2}(\frac{\partial w}{\partial y}+\frac{\partial v}{\partial z})=\frac{1}{2}{\gamma }_{yz}$$

$${\epsilon }_{xz}=\frac{1}{2}(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x})=\frac{1}{2}{\gamma }_{xz}$$

 

이를 앞서 언급한 tensor notation으로 표현하자면 아래와 같다.

(이때 shear strain rate in Cartesian coordinates이다.)

$${\epsilon }_{ij}=\frac{1}{2}({\partial }_i{u}_j+{\partial }_j{u}_i)$$

 

Furtherfmore:

$$[\epsilon ]=\left[\begin{array}{ccc}{\epsilon }_{xx}& {\epsilon }_{xy}& {\epsilon }_{xz}\\ {\epsilon }_{yx}& {\epsilon }_{yy}& {\epsilon }_{yz}\\ {\epsilon }_{zx}& {\epsilon }_{zy}& {\epsilon }_{zz}\end{array}\right]=\left[\begin{array}{ccc}\frac{\partial u}{\partial x}& \frac{\partial u}{\partial y}& \frac{\partial u}{\partial z}\\ \frac{\partial v}{\partial x}& \frac{\partial v}{\partial y}& \frac{\partial v}{\partial z}\\ \frac{\partial w}{\partial x}& \frac{\partial w}{\partial y}& \frac{\partial w}{\partial z}\end{array}\right]$$

 

$$[{\gamma }_{ij}]=\left[\begin{array}{ccc}0& {\gamma }_{xy}& {\gamma }_{xz}\\ {\gamma }_{yx}& 0& {\gamma }_{yz}\\ {\gamma }_{zx}& {\gamma }_{zy}& 0\end{array}\right]=\left[\begin{array}{ccc}0& \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}& \frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}\\ \frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}& 0& \frac{\partial v}{\partial z}+\frac{\partial w}{\partial y}\\ \frac{\partial w}{\partial x}+\frac{\partial u}{\partial z}& \frac{\partial w}{\partial y}+\frac{\partial v}{\partial z}& 0\end{array}\right]$$

 

Fluid mechanics 3rd edtion p.152 - p.154

컴퓨터원용 고체역학 Mechanics of SOLIDS p.547 - p.533