대학원 공부노트
Hasegawa(1969) 1번 식 해설 2편 본문

지난 글에 이어 다룰 내용은 poisson's ratio부터 시작된다.
$$\nu=-\frac{\varepsilon_{xx}}{\varepsilon_{yy}}$$
$$\Rightarrow \varepsilon_{yy}=-\frac{1}{\nu}\varepsilon_{xx}\cdots (1)$$
$$\sigma_{yy}=E\varepsilon_{yy}$$
$$\Rightarrow \varepsilon_{yy}=\frac{1}{E}\sigma_{yy}\cdots (2)$$
식(1)에 식(2)를 대입하면 아래와 같은 식을 구할 수 있다.
$$\varepsilon_{yy}=-\frac{1}{\nu}\varepsilon_{xx}=\frac{1}{E}\sigma_{yy}$$
이는 \(y\) 방향으로 수축할 때 \(x\) 방향으로 신장된 길이(\(\varepsilon_{yy}\))이다.
물론 그 반대도 가능하다. \(y\) 방향으로 신장될 때 \(x\) 방향으로 수축된 길이라 보아도 된다.
그리고 해당 개념을 동일하게 3차원으로 확장하면 각각의 방향에 대한 변형률을 알 수 있다.
$$\varepsilon_{xx}=\frac{1}{E}\sigma_{xx}$$
$$\varepsilon_{xx}=-\frac{\nu}{E}\sigma_{yy}$$
$$\varepsilon_{xx}=-\frac{\nu}{E}\sigma_{zz}$$
그리고 3차원으로 생각하면 \(x\)방향으로 인장할 때 \(y-z\) 방향으로 수축이 일어나므로 식은 아래와 같아진다.
$$\varepsilon_{xx}=\frac{1}{E}\left[\sigma_{xx}-\nu(\sigma_{yy}+\sigma_{zz})\right]\cdots(3)$$
동일한 개념을 \(y\),와 \(z\) 방향으로도 적용해주면 다음과 같다.
$$\varepsilon_{yy}=\frac{1}{E}\left[\sigma_{yy}-\nu(\sigma_{xx}+\sigma_{zz})\right]$$
$$\varepsilon_{zz}=\frac{1}{E}\left[\sigma_{yy}-\nu(\sigma_{xx}+\sigma_{yy})\right]$$
그리고 식(3)을 \(\sigma_{xx}\)에 대해 정리한다.
그래야만 앞에서 이전 글에서 살펴보았던 행렬을 만들 수 있다.
$$\varepsilon_{xx}=\frac{1}{E}\left[\sigma_{xx}-\nu(\sigma_{yy}+\sigma_{zz})\right]\cdots(3)$$
$$\varepsilon_{xx}=\frac{1}{E}\left[(1+\nu)\sigma_{xx}-\nu(\sigma_{xx}+\sigma_{yy}+\sigma_{zz})\right]$$
$$E\varepsilon_{xx}=(1+\nu)\sigma_{xx}-\nu(\sigma_{xx}+\sigma_{yy}+\sigma_{zz})$$
$$E\varepsilon_{xx}+\nu(\sigma_{xx}+\sigma_{yy}+\sigma_{zz})=(1+\nu)\sigma_{xx}$$
$$\sigma_{xx}=\frac{E}{1+\nu}\varepsilon_{xx}+\frac{\nu}{1+\nu}(\sigma_{xx}+\sigma_{yy}+\sigma_{zz})\cdots (4)$$
이제 \(\sigma_{xx}+\sigma_{yy}+\sigma_{zz}\) 항만 잘 정리하면 된다.
앞에서 구했던 식들을 사용하도록 하자.
$$\varepsilon_{xx}+\varepsilon_{yy}+\varepsilon_{zz}=\frac{1}{E}\left[(1+\nu)(\sigma_{xx}+\sigma_{yy}+\sigma_{zz})-3\nu(\sigma_{xx}+\sigma_{yy}+\sigma_{zz}\right]$$
$$=\frac{1-2\nu}{E}(\sigma_{xx}+\sigma_{yy}+\sigma_{zz})$$
$$\sigma_{xx}+\sigma_{yy}+\sigma_{zz}=\frac{E}{1-2\nu}(\varepsilon_{xx}+\varepsilon_{yy}+\varepsilon_{zz})\cdots(5)$$
식(4)에 식(5)를 넣어주면 아래와 같이 정리할 수 있다.
$$\sigma_{xx}=\frac{E}{1+\nu}\varepsilon_{xx}+\frac{\nu E}{(1+\nu)(1-2\nu)}(\varepsilon_{xx}+\varepsilon_{yy}+\varepsilon_{zz})$$
그리고 계수 간의 관계(Lamé parameter)를 적용해주면 아래와 같이 정리할 수 있다.
[해당 관계식 중 하나는 고체역학 566 페이지에 유도 방법이 나오나 다른 하나는 도무지 모르겠다.]
$$2\mu=2G=\frac{E}{1+\nu}~~~~~\lambda=\frac{E\nu}{(1+\nu)(1-2\nu)}$$
$$\sigma_{xx}=2\mu\varepsilon_{xx}+\lambda(\varepsilon_{xx}+\varepsilon_{yy}+\varepsilon_{zz})\cdots(6)$$
자연스럽게 나머지 방향에 대해서도 아래와 같이 정리할 수 있다.
$$\sigma_{yy}=2\mu\varepsilon_{yy}+\lambda(\varepsilon_{xx}+\varepsilon_{yy}+\varepsilon_{zz})\cdots(6)$$
$$\sigma_{zz}=2\mu\varepsilon_{zz}+\lambda(\varepsilon_{xx}+\varepsilon_{yy}+\varepsilon_{zz})\cdots(6)$$
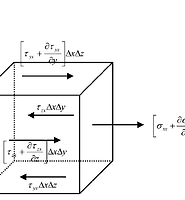
위에서는 대각선 행렬값들을 구하였다. 이제는 나머지 항들에 대해서도 계산을 해준다.
$$\sigma_{xy}=\tau_{xy}=G\gamma_{xy}\cdots(7)$$
$$2\tau_{xy}=2G\gamma_{xy}$$
이때 지난 글에서 유도하였던 아래 식을 적용한다.
$$\varepsilon_{xy}=\frac{1}{2}\gamma_{xy}=\frac{1}{2}\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)$$
$$\gamma_{xy}=2\varepsilon_{xy}\cdots(8)$$
식 (7)에 식 (8)을 대입해주면
$$2\sigma_{xy}=2\tau_{xy}=4G\varepsilon_{xy}$$
$$\sigma_{xy}=2G\varepsilon_{xy}=2\mu\varepsilon_{xy}~~~(\mu=G)$$
이제 지금까지 구한 내용들을 행렬로 정리해주면 아래와 같다.
$$\begin{bmatrix} \sigma_{11} & \sigma_{12} & \sigma_{13}\\ \sigma_{21} & \sigma_{22} & \sigma_{23}\\ \sigma_{31} & \sigma_{32} & \sigma_{33}\\ \end{bmatrix} = 2\mu \begin{bmatrix} \varepsilon_{11} & \varepsilon_{12} & \varepsilon_{13}\\ \varepsilon_{21} & \varepsilon_{22} & \varepsilon_{23}\\ \varepsilon_{31} & \varepsilon_{32} & \varepsilon_{33}\\ \end{bmatrix} +\lambda \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end{bmatrix} (\varepsilon_{11}+\varepsilon_{22}+\varepsilon_{33})$$
그리고 행렬을 앞서 도입한 tensor notation으로 표현하면 아래와 같아진다.
$$\tau_{ij}=2\mu\varepsilon_{ij}+\lambda \textbf{I} (\varepsilon_{11}+\varepsilon_{22}+\varepsilon_{zz})$$
그리고 kronecker delta와 einstein notation을 도입하면 조금 더 간결하게 표현할 수 있다.
$$\tau_{ij}=\lambda\delta_{ij}\sum_{k}{\varepsilon_{kk}}+2\mu\varepsilon_{ij}$$
\(\blacksquare\)
참고로 kronecker delta와 einstein notation은 아래와 같다.
$$ \begin{bmatrix} \delta_{11} & \delta_{12} & \delta_{13}\\ \delta_{21} & \delta_{22} & \delta_{23}\\ \delta_{31} & \delta_{32} & \delta_{33}\\ \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end{bmatrix}$$
$$\delta_{ij}=\begin{cases} 1 ~~(m=n) \\ 2 ~~(m\neq n) \end{cases}$$
$$\sum_{k}{\varepsilon_{kk}}=\varepsilon_{11}+\varepsilon_{22}+\varepsilon_{33}$$
Reference
Wikipedia, Hooke's law
Wikipedia, Lamé parameter
Wikipedia, Identity matrix
Wikipedia, Trace
'대학원 공부 > Hasegawa' 카테고리의 다른 글
| Hasegawa equation (0) | 2022.08.05 |
|---|---|
| Hasegawa(1969) 1번 식 해설 4편(완) (0) | 2022.07.31 |
| Hasegawa(1969) 1번 식 해설 3편 (0) | 2022.07.29 |
| Hasegawa(1969) 1번 식 해설 1편 (0) | 2022.07.25 |
| Hasegawa(1969) 8번, 10번, 11식 해설 (0) | 2022.07.20 |