Hasegawa(1969) 5번 식 해설

$$p=A e^{i(\omega t - kx)}=Ae^{i\omega}e^{-ikx}=Ae^{i\omega t}e^{-ikr\cos\theta}$$

$$(x=r\cos\theta)$$

 

이번 페이지에서 다룰 내용은 Fourier-Legendre series를 다룰 예정입니다.

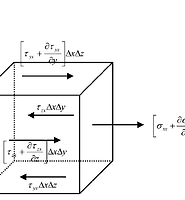
목표는 아래 두 식을 유도해내는 것이에요.

$$f(x)=\sum_{n=0}^{\infty}{a_{n}P_{n}}$$

$$a_{m}=\frac{2m+1}{2}\int_{-1}^{1}{f(x)P_{m}(x)dx}$$

 

---

Step 1: Legendre Polynomial

To derive above equations, we need 'Legendre polynomial'

$$P_{n}(x)=\sum_{m=0}^{M}{(-1)^{m}\frac{(2n-2m)!}{2^{n}m!(n-m)!(n-2m)!}x^{n-2m}}$$

 

Similarily, we can express \(f(x)\) with Legendre polynomial

$$f(x)=\sum_{n=0}^{\infty}{a_{n}P_{n}(x)}$$

 

And coefficient \(a_{n}\) can be derived by using orthogonality

(We derived/studied 'orthogonality' before.)

$$\int_{-1}^{1}{r(x)P_{m}(x)P_{n}(x)}=0~~(m\neq n)$$

 

$$f(x)=\sum_{n=0}^{\infty}{a_{n}P_{n}(x)}$$

$$r(x){\color{blue}f(x)}P_{m}(x)={\color{blue}\sum_{n=0}^{\infty}}{{\color{blue}a_{n}P_{n}(x)}r(x)P_{m}(x)}$$

$$\int_{-1}^{1}{r(x)f(x)P_{m}(x)dx}=\int_{-1}^{1}{\sum_{n=0}^{\infty}{a_{n}r(x)P_{n}(x)P_{m}(x)}dx}\cdots(1)$$

 

According to orthogonality under \(m\neq n)

$$\int_{-1}^{1}{P_{n}(x)P_{m}(x)dx}=0$$

 

So, equation (1) will be...

$$\int_{-1}^{1}{r(x)f(x)P_{m}(x)dx}=a_{n}\int_{-1}^{1}{r(x)P_{m}(x)P_{n}(x)dx}~~~~(m=n)$$

$$a_{n}=\frac{\int_{-1}^{1}{r(x)f(x)P_{m}(x)dx}}{\int_{-1}^{1}{r(x)P_{m}^{2}(x)dx}}$$

 

Step 2: Rodrigues formula

We derived/studied 'Rodrigues formula' before.

$$P_{n}(x)=\frac{1}{2^{n}n!}\frac{d^{n}}{dx^{n}}(x^{2}-1)^{n}$$

 

Let's put this equation in our integral form.

$$\int_{-1}^{1}{P_{n}^{2}(x)dx}=\frac{1}{2^{2n}(n!)^{2}}\int_{-1}^{1}{\frac{d^{n}}{dx^{n}}(x^{2}-1)^{n}\frac{d^{n}}{dx^{n}}(x^{2}-1)^{n}dx}$$

 

As it is too complex to solve at once, use integration by parts.

 

 

 

Reference

Advanced Engineering Mathematics p.178 SEC 5.2 Legendre's equation. Legendre polynomials